스프링의 힘 계산 방법에 대해서
스프링의 힘 계산 방법
스프링은 늘어나는/축소 등 변형된 힘을 축적하여 그 반발력을 작용으로 하는 기계 요소입니다.
그 변형은 "휘어짐"의 양으로 나타나는 스프링의 "탄성 에너지"이며, 반발력은 "스프링레이트"나 "스프링레이트"라고 하는 "스프링 정수(스프링 정수)"로 나타납니다.
그리고 이러한 값으로 스프링의 힘은 결정됩니다.
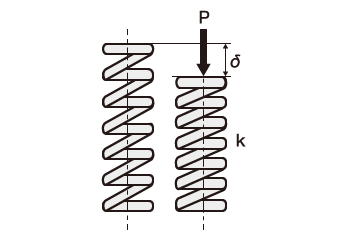
예를 들어, 스프링 정수는 스프링을 일정한 길이만큼 신축(변위)시킬 때 필요한 힘을 말합니다.
스프링을 1mm 단축하거나 늘릴 때 필요한 힘이 4N이면,

됩니다.
단위는, 이전에는 kg(킬로그램)이었지만, 지금은 "N(뉴턴)/mm"입니다.
또, 신축시키는 양(변위)은 "휘어짐"입니다.
여기에서는 이들 값을 구하는 방법을 통해 각각의 관계를 설명합니다.
휨를 구하다
신축하는 양(변위)은 "휘어짐"이라고 하며, 휘어짐은 이하의 공식으로 나타납니다.

δ:용수철의 굴곡
G: 횡탄성계수
(재료 고유의 값 스테인리스(SUS302)는 68,500, 피아노(경강)선은 78,500)
Na: 유효 권수
D: 코일 평균 지름
d: 선경
P: 스프링에 가해지는 하중

스프링 상수(스프링 레이트/스프링 레이트)를 구한다
스프링 정수는 그 스프링의 경도(반발력의 강도)를 나타냅니다.
일반적으로 선재가 부드러운 스프링은 줄어들기 쉽고, 딱딱한 스프링은 줄어들기 어렵습니다.
그래서 스프링의 경도를 수치화하기 위해 스프링을 1mm 단축하기 위해 필요한 하중을 계측하여 수치 표기한 것이 스프링 정수입니다.
스프링 정수는 후크의 법칙에서 구할 수 있습니다.
후쿠의 법칙:
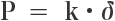
스프링 정수:
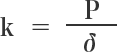
누르는 스프링의 경우:

P: 스프링에 가해지는 하중
용수철의 굴곡
G: 횡탄성계수
(재료 고유의 값 스테인리스(SUS302)는 68,500, 피아노(경강)선은 78,500)
Na: 유효 권수
D: 코일 평균 지름
d: 선경
스프링의 탄성 에너지를 구하다
늘어나거나 줄어드는 등 스프링이 변형되어 축적하는 힘을 '스프링의 탄성 에너지' 또는 '탄성력에 의한 위치 에너지'라고 합니다.
힘은 스프링의 성장에 비례하여 스프링의 성장이 클수록 힘이 커지고, 그 크기는 직선적으로 바뀜니다.
단, 어떤 스프링도 반드시 탄성에는 한계가 있으며, 한계를 넘는 하중이 걸리면 원래의 형태로 돌아가지 않게 됩니다.
이 돌아오지 않게 되는 현상을 '소성'이라고 합니다.
즉, 스프링은 탄성이 미치는 범위의 하중에서 사용해야 하며, 소성의 범위까지 하중을 가해서는 안됩니다.
이것은 스프링의 종류에 관계없이 모든 스프링에 공통의 규칙입니다.
탄성에너지를 구하는 식은 다음과 같습니다.
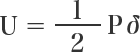
여기에 'P=kδ'를 대입하면
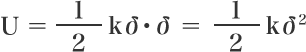
U: 탄성에너지(N·mm=J)
k: 스프링 상수
P: 스프링에 가해지는 하중(N)
δ: 스프링의 굴곡(mm)
단위 부피당 탄성 에너지를 구하다
스프링의 성능을 나타내는 척도로서 "단위 부피당 탄성 에너지"가 있습니다.
이것은 스프링을 하나의 둥근 막대라고 생각하고, 그 부피로 스프링의 충격 흡수력을 구하는 방법입니다.
이 수치가 클수록 작은 부피로 큰 에너지를 흡수할 수 있음을 나타냅니다.
단위 부피당 탄성 에너지는 아래의 식으로 구할 수 있습니다.

u: 단위 부피당 탄성 에너지(J/mm) 2 )
U: 탄성에너지(N·mm=J)
V: 부피*
* 스프링의 부피(V) 구하는 법
V = Lπr2
L: 선재의 길이(내경과 외경의 평균×감는 수) r: 스프링의 반경(선경의 1/2)
권밀도를 고려할 경우에는 다음 계산이 더 필요하다.
V = V/cosθ
θ: 스프링 각도(rad) θ=arcsin(스프링 길이/L)
'수질관련용어' 카테고리의 다른 글
| 스핀코팅 장치는? (0) | 2022.10.04 |
|---|---|
| 저항 가열형 진공 증착법에 대해서 (0) | 2022.10.04 |
| 스프링의 움직임을 제어 (1) | 2022.10.04 |
| vacuum gauge 종류에 대해서 (1) | 2022.10.04 |
| 기압에 대해서 (0) | 2022.10.04 |
