굴절계의 원리는 무엇인가?
굴절계의 원리는 무엇인가?
스넬의 법칙
스넬의 법칙은 근처의 두 매체를 통해 빛의 통과를 기술하는 법칙이다. 굴절의 법칙으로도 알려져 있다.
굴절계
n1×sin1=n2×sin2
n1: 매체에 들어갈 때 빛의 굴절률
θ1: 입사각
n2: 매체를 배출할 때 빛의 굴절률
θ2: 발생각
사인(sin)은 각도를 이용하여 직각 삼각형의 높이를 나타내는 변환 코드다.
특수한 경우 ... sin0° = 0, sin30° = 1/2, sin45° = √2/2, sin60° = √3/2, sin90° = 1
As θ increases, sinθ also increases.
빛의 특성
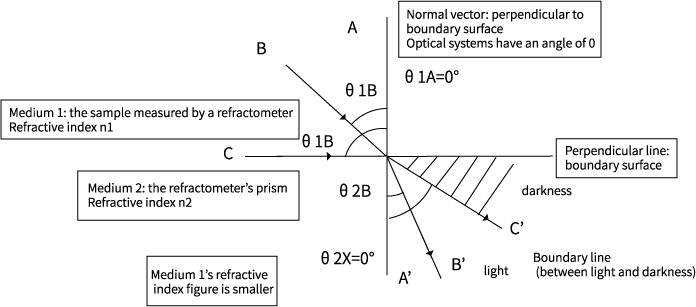
매질의 경계면에 수직인 빛(0°)이 굴절 없이 직진한다.
빛의 경계 표면은 높은 굴절률로 매질 측면에 가시화된다.
빛의 경로(화살표)가 역류하더라도 빛은 같은 경로(각도)를 이동한다(빛의 역전성)
레이 A
광선 A를 고려한다.
n1Sinθ1A =n2Sinθ2A'
n1×0 =n2×신기2A'
0 =n2×신기2A
θ1A는 0이므로 n1의 값에 관계없이 0으로 나온다. n2×sinθ2를 만드는 방법A'는 0, equal2A'도 0이어야 한다. 따라서 바로 위에서 들어오는 빛은 바로 아래에서 방출될 것이다. 일반 벡터 조명은 일반 벡터로 나간다.
레이 B
레이 B를 고려한다.
n1Sinθ1B=n2Sinθ2B'
n2가 n1보다 크다는 점을 감안하면 sin'2B'는 sinθ1B보다 작아야 하며 그렇지 않으면 방정식의 양면이 같지 않을 것이다. 축음기를 작게 하려면 θ은 작아야 하며, θ2B'는 θ1B보다 작은 발생 각도가 될 것이다. 광선 B와 같은 비스듬한 광선이 굴절되어 다음 매체로 들어간다.
레이 C
레이 C를 고려한다.
레이 C는 일반 벡터로부터 90° 떨어진 곳에 있는 광선이며, 두 매체 사이의 경계 표면에 있다.
경계 표면의 빛에 무슨 일이 일어나는지 알 수 없는 경우가 많지만, 적어도 89.9 °의 광선이 존재한다. 90°(90.000001°) 이상의 각도를 가진 조명 중2에서 나오는 빛이기 때문에 이 빛을 무시한다면 90°의 각도를 가진 광선이 가장 큰 각이다.
n1Sinθ1C =n2Sinθ2C'
n1Sin90° =n2Sinθ2C'
n1×1 =n2Sinθ2C
n1 =n2Sinθ2C'
sin90° = 1을 사용하면 1의 곱셈이 사라진다. 공식의 왼쪽이 n1이 된다.
n2는 이미 알려진 프리즘의 굴절률이다.
θ2는 굴절각이며 n1을 측정해야 한다.
굴절지수는 입사각 90°(프리즘과 직각)의 빛의 출현 각도를 측정하여 측정할 수 있다.
굴절계는 빛의 각도를 측정하고 그 각도를 굴절률로 변환하는 장치다.
